高校教师申请开通试用请联系微信+电话 136-9329-0406 开通项目权限。登录网址:http://idatacoding.cn
数学是 AI 的底层逻辑支柱,动手编程则是 AI 能力落地的关键桥梁。本项目的主要目的是帮助学习者在这两方面进行融会贯通。项目通过 Python 代码实现、案例演练帮助学习者具象化理解人工智能中涉及的抽象数学基础理论,系统掌握AI的数学基础知识。
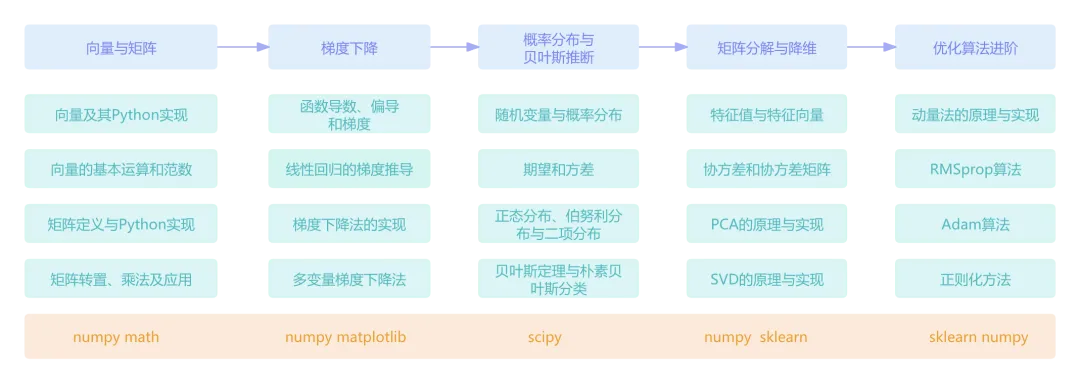
锻炼能力:线性代数; 概率论与统计学; Python实践
实践工具:Numpy; Matplotlib; Scipy; Pandas; Sklearn
前置基础:Python基础; 微积分基础; Matplotlib基础
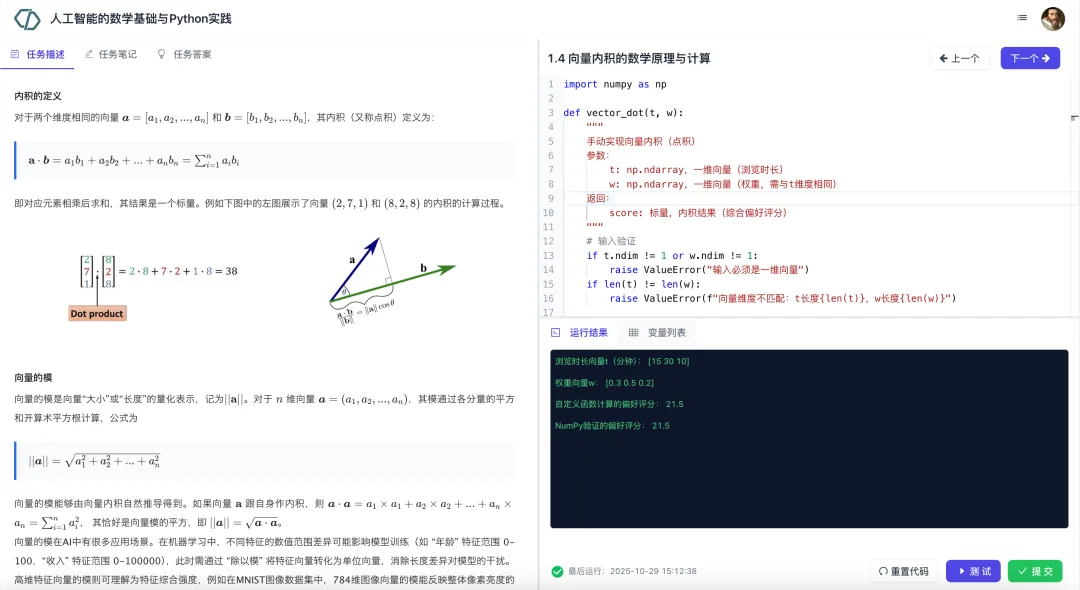
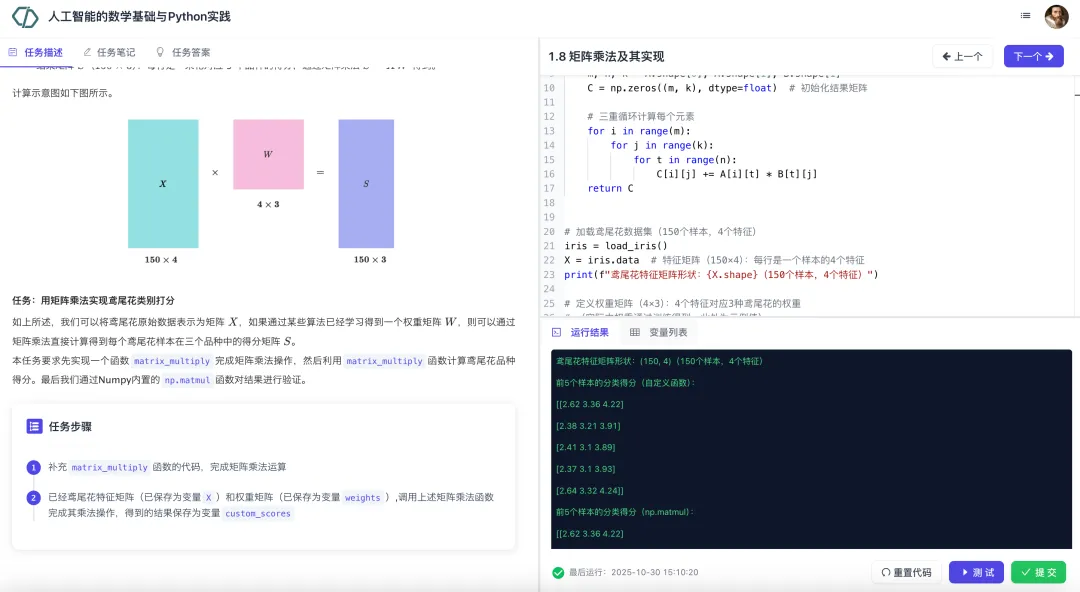
本模块介绍向量和矩阵的基本知识。向量部分我们先从其数学定义和Python表示开始,依次介绍向量的线性预算、向量内积、向量范数等。矩阵部分先介绍其定义和Python实现,讲解矩阵转置及其性质、随后介绍矩阵乘法、矩阵向量乘法。最后介绍矩阵乘法的两个重要应用:批量计算向量内积和余弦相似度。

实训任务展示:
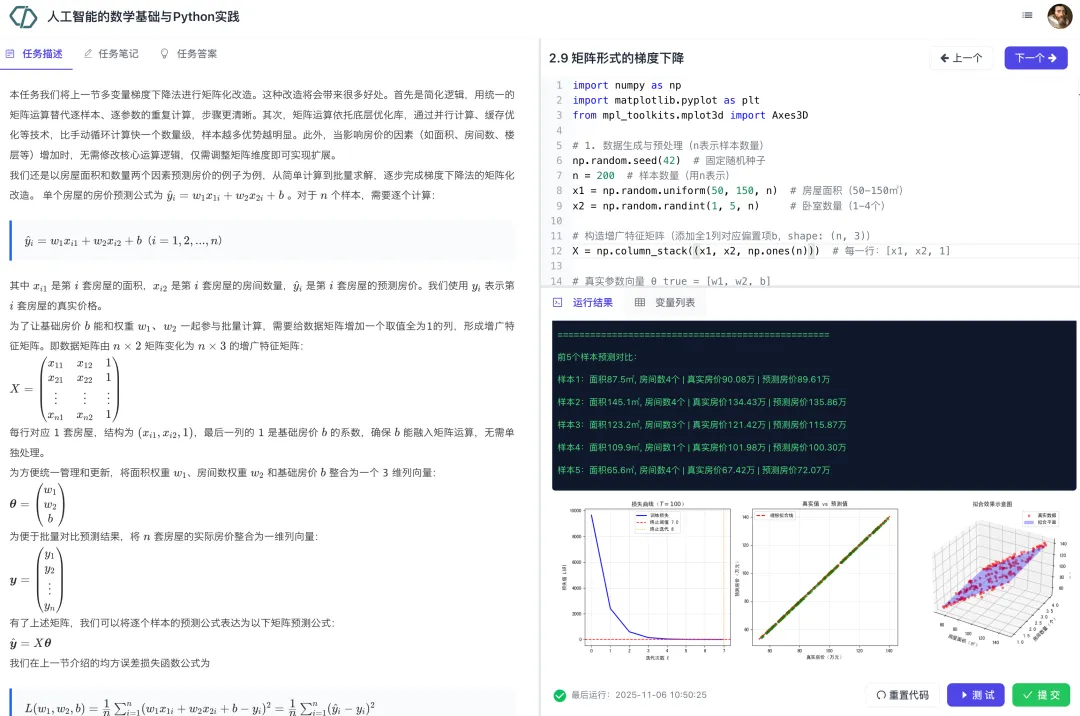
本模块先介绍函数的导数和梯度概念,进而讲解梯度的数值计算方法。介绍完梯度的基本概念后,以线性回归这个简单问题为例,帮助学员构建AI模型中的损失函数的概念。通过对损失函数最优化问题的求解,自然引出梯度下降法的原理和过程。

实训任务展示:
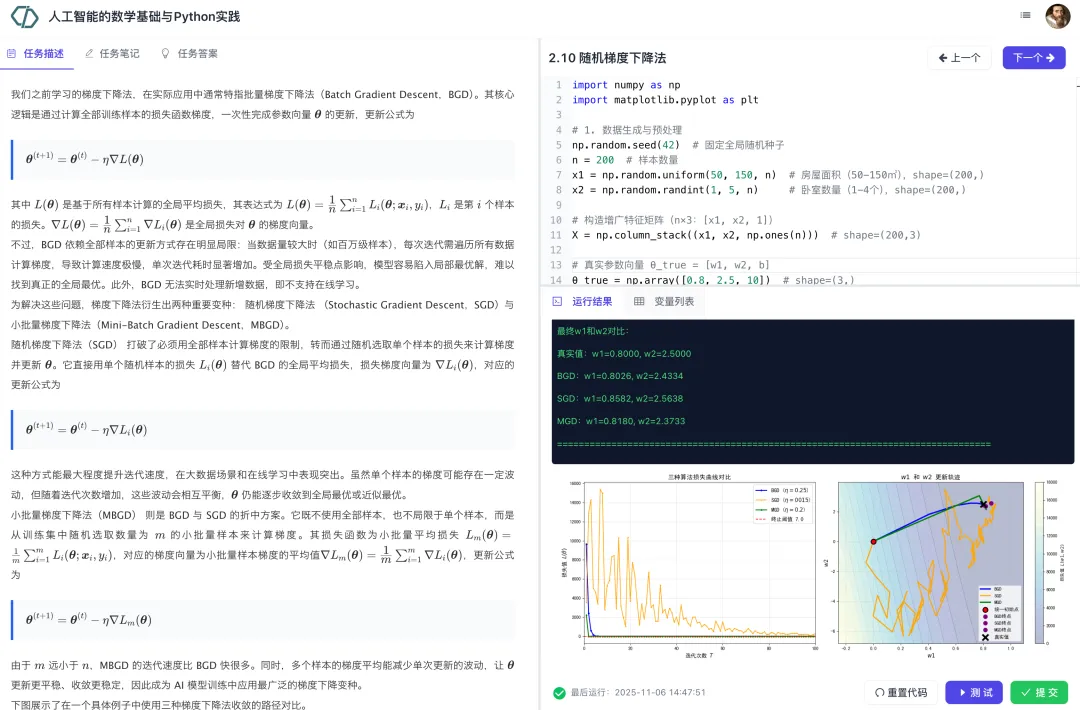
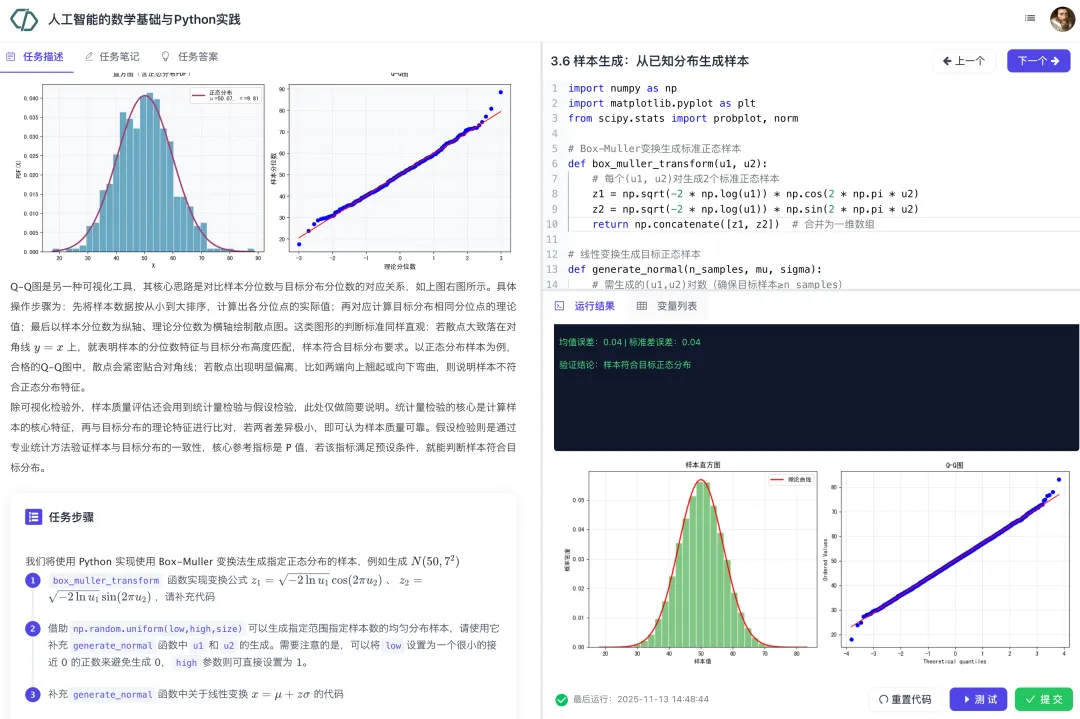
本模块主要讲解常见概率分布特性与贝叶斯定理推导逻辑。我们首先介绍随机变量、概率分布、期望和方差等基本概念。然后介绍了离散分布(伯努利分布、二项分布、类别分布和多项分布)、连续型分布(均匀分布、正态分布、指数分布、对数正态分布、学生t分布和贝塔分布)。随后介绍已知分布生成样本的方法以及基于样本和分布的参数估计方法。在贝叶斯推断部分,我们先讲解贝叶斯定理、然后介绍条件独立性假设,最后介绍朴素贝叶斯分类算法。最后我们介绍基于贝叶斯推断的极大后验估计方法。

实训任务展示:
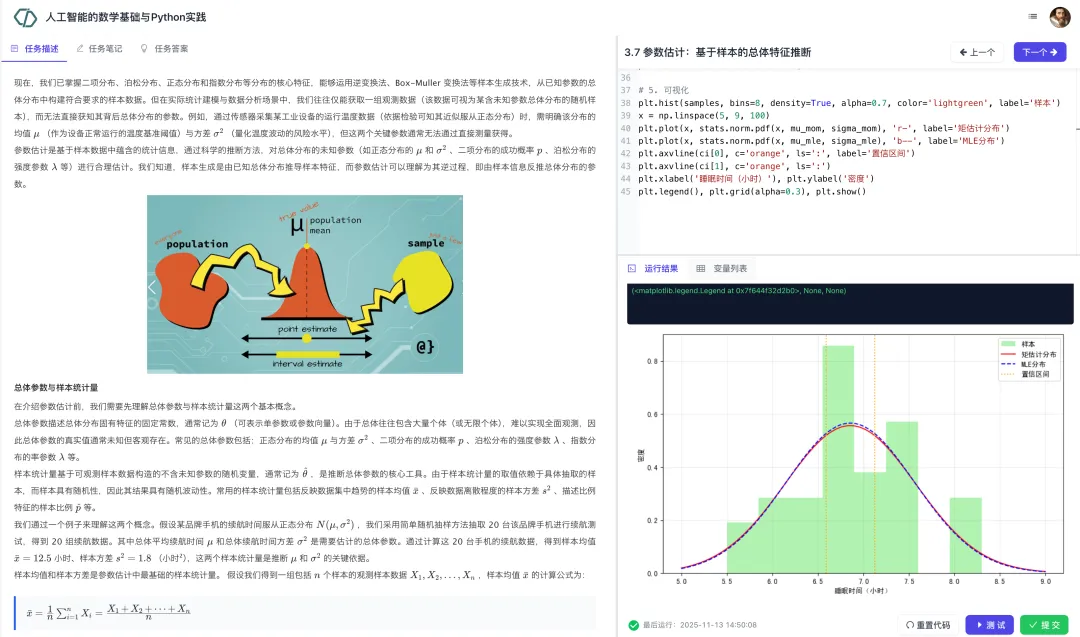
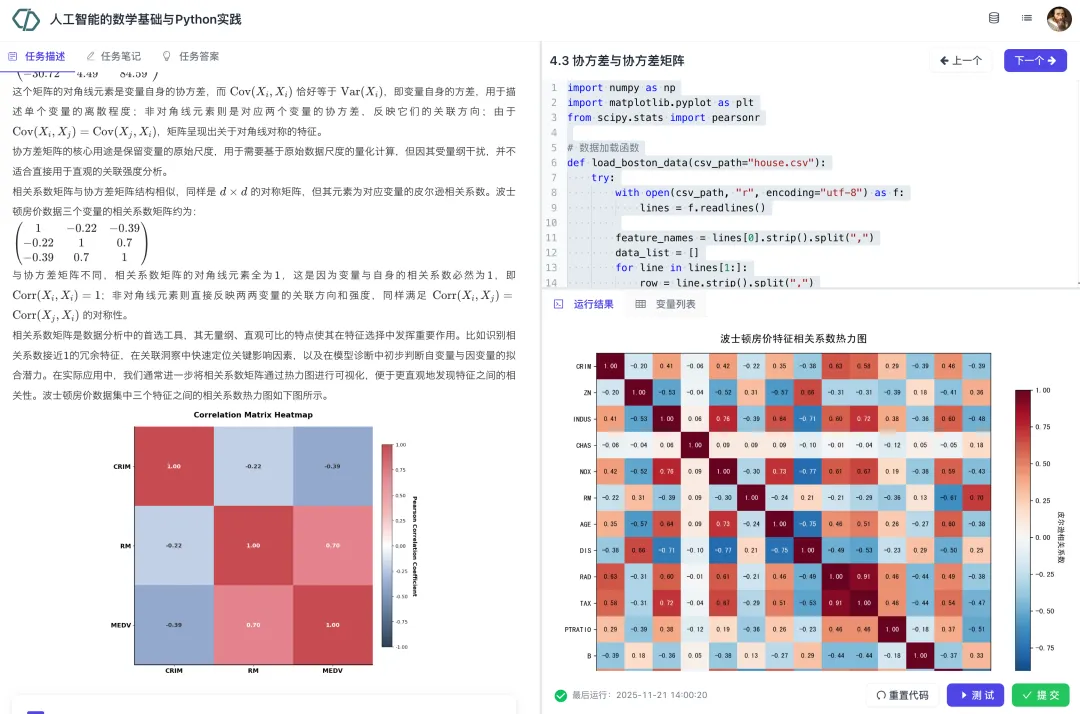
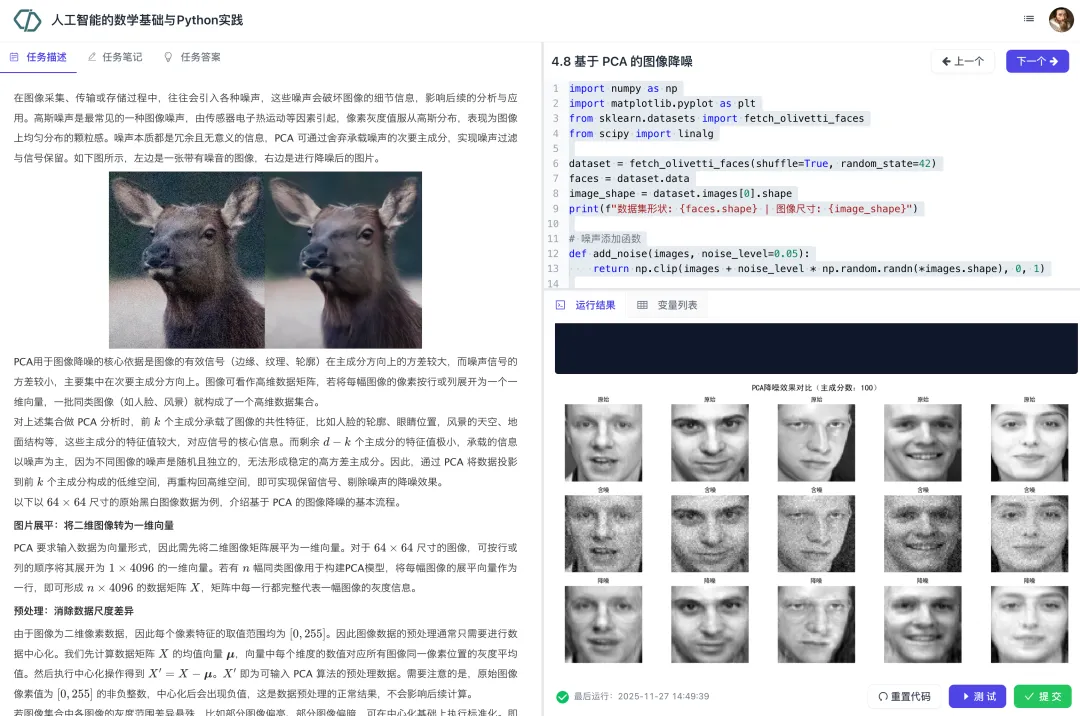
本模块先讲解特征值、特征向量、协方差和协方差矩阵等基本概念。然后介绍特征值分解,以及基于特征值分解的PCA算法。随后介绍如何基于PCA进行数据降维、高维数据重构和图像降噪。最后我们讲解了奇异值分解及其在图像压缩中的应用。在讲解数学原理的同时,依托 NumPy 开展实践操作,帮助学习者掌握高维数据压缩与特征提取技术。

实训任务展示:
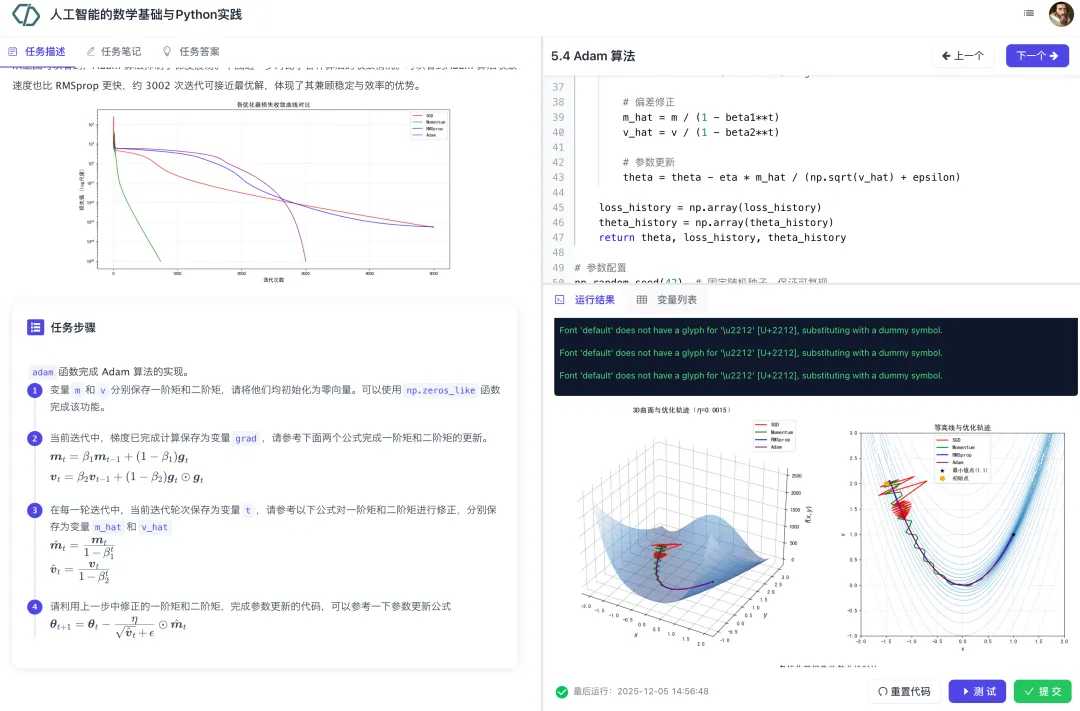
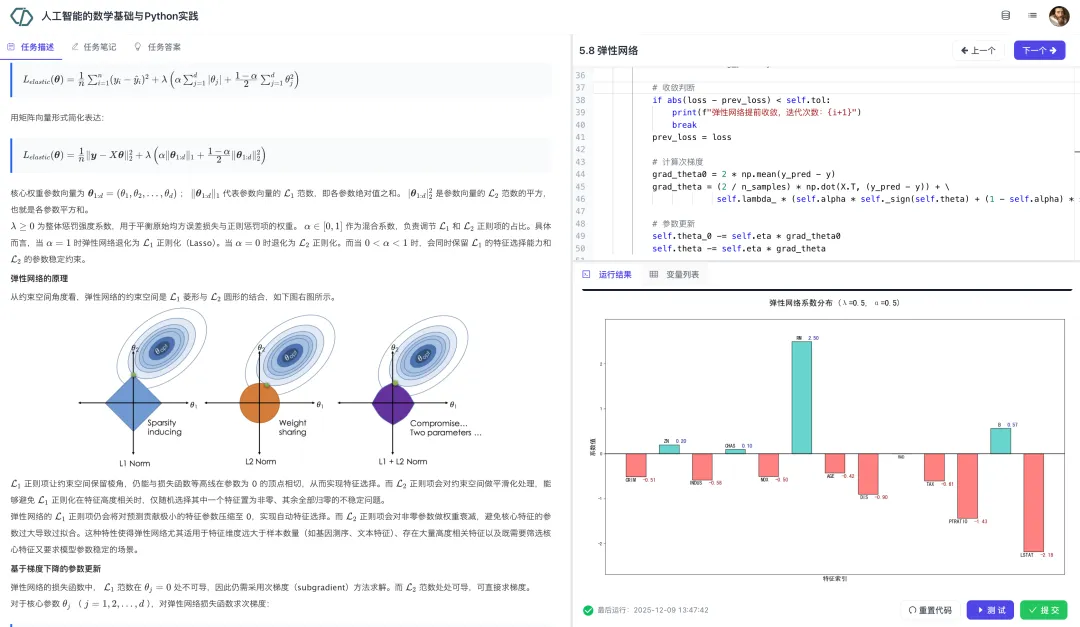
本模块主要讲解突破上述局限的一些高阶优化方法。我们先讲解动量法、RMSprop 算法和 Adam 等进梯度下降法的改进算法。随后我们介绍过拟合的概念,以及正则化这种解决过拟合的优化策略,包括 正则化、 正则化和弹性网络。

实训任务展示:






.png)


